| . . . |
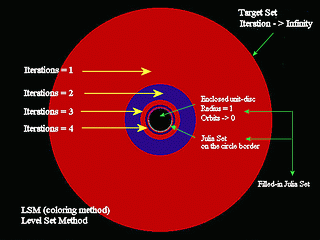
Picture 1, "C=0 Distant", shows the dynamical process of: z -> z^2 (that's the dynamical process z -> z^2 + c where c = 0). The small black disk contains those "z" whose orbits never reach infinity under iteration. They are contained within a circle of radius 1. Inside the disc the orbit tends to zero. The Julia set is the border between those "z" tending to infinity, and those "z" tending to zero. Those "z" situated exactly on this border (the circle), never leave the circle. The Julia set together with eventually enclosed regions, in our case the enclosed unit-disc is called filled-in Julia set. Outside the closed unit-disc the z - plane, that is the dynamical plane, is decomposed after the number of iteration required taking the orbit of "z" beyond a radius of 10 (the radius must be at least 2, but any bigger radius will fit). The area outside this radius is called the target set here colored black. The area followed immediately inside, colored red, is the first level set, containing those "z" requiring 1 iteration to reach the target set. The next area, colored dark-blue, is the second level set, containing those "z" requiring 2 iterations to reach the target set etc. There are an infinite number of level sets, coming closer and closer to the filled-in Julia set. This colored method, Level Set Method (LSM), is the simplest method of coloring escape fractals. Picture 2, "C=0", shows the normal magnification. Regards, Ingvar Ingvar Kullberg, December 2001 www.come.to/kullberg / http://come.to/kullberg |