| . . . |
How to make a long story short?
| Sign | Name | Function |
| + | Plus | Addition |
| - | Minus | Subtraction |
| * | Asterisk | Multiplication |
| / | Slash | Division |
| ^ | Circumflex | Raise to Power |
 In chapter I have written some long lines with a chain multiplication of the letter "Z" like this:
In chapter I have written some long lines with a chain multiplication of the letter "Z" like this:
Z = Z * Z * Z * Z * Z * Z * Z + C
What we have here is the letter Z multiplied by itself 7 times. This could be written in a much shorter way, using a computer-math convention - the circumflex sign. This sign is seen at the bottom of the left table in red. You write the letter Z, then the circumflex sign, and then the number of times that Z appears in the multiplication chain. So this very long line of 7 "Z" letters with asterisks between them could be written in short like this:
Z = Z ^ 7
How to make more complex patterns?
| Function | Name |
| sin(Z) | sinus |
| cos(Z) | cosinus |
| tan(Z) | tangents |
| cotan(Z) | cotangents |
| asin(Z) | arc-sinus |
| acos(Z) | arc-cosinus |
| atan(Z) | arc-tangents |
 Up to now we have seen the four math signs that we have used between the "Z"s and "C"s. These signs are called math "operators" because they are causing the four math operations: add, subtract, multiply and divide. Now to add some more interesting patterns to the fractal we need to increase the power of the curves, which could be achieved by adding the "trigonometric" functions. Don't be impressed by the titles and names - just use these function instead of the letters "Z" or "C" or in place of a math sign. Just try any one you wish in any place and enjoy the graphical results. In pictures 7 and 8 you can see how I have used the sinus function in picture 7 and the atan function in picture 8. In both cases the trig function was added with the multiplication operator. Please note, that all trig function have brackets. Inside the brackets you have to put a letter, either "Z" or "C". You can also insert a number into the brackets, but then the string: sin(123) is a constant number, and the fractal formula will cause a change along axis and zooming but not of patterns.
Up to now we have seen the four math signs that we have used between the "Z"s and "C"s. These signs are called math "operators" because they are causing the four math operations: add, subtract, multiply and divide. Now to add some more interesting patterns to the fractal we need to increase the power of the curves, which could be achieved by adding the "trigonometric" functions. Don't be impressed by the titles and names - just use these function instead of the letters "Z" or "C" or in place of a math sign. Just try any one you wish in any place and enjoy the graphical results. In pictures 7 and 8 you can see how I have used the sinus function in picture 7 and the atan function in picture 8. In both cases the trig function was added with the multiplication operator. Please note, that all trig function have brackets. Inside the brackets you have to put a letter, either "Z" or "C". You can also insert a number into the brackets, but then the string: sin(123) is a constant number, and the fractal formula will cause a change along axis and zooming but not of patterns.

Picture 7.
Formula: Z = Z ^ 2 * sin(Z) + C
|

Picture 8.
Formula: Z = Z ^ 2 * atan(C) + C
|
How to bend the curves even more?
| Function | Name |
| sinh(Z) | sinus-hyperbolic |
| cosh(Z) | cosinus-hyperbolic |
| tanh(Z) | tangents-hyperbolic |
| cotanh(Z) | cotangents-hyperbolic |
| asinh(Z) | arc-sinus-hyperbolic |
| acosh(Z) | arc-cosinus-hyperbolic |
| atanh(Z) | arc-tangents-hyperbolic |
 Here is the last set of trig functions, this time they are called: hyperbolic functions. Again don't pay attention to names, just use these functions as you have used the previous ones. You can use the trig function at any place in the formula line, replacing either or both "Z" and "C".
Here is the last set of trig functions, this time they are called: hyperbolic functions. Again don't pay attention to names, just use these functions as you have used the previous ones. You can use the trig function at any place in the formula line, replacing either or both "Z" and "C".
In picture 9 I used the sinh(Z) as the power of "Z". The formula looks like this:
Z = Z ^ sinh(Z) + C
In picture 10 I used the atanh(C) as the power of "Z". The formula looks like this:
Z = Z ^ atanh(C) + C
Please notice that in picture 9 the variable inside the trig function sinh() is "Z" while in picture 10 the variable inside the trig function atanh() is "C".

Picture 9.
Formula: Z = Z ^ sinh(Z) + C
|

Picture 10.
Formula: Z = Z ^ atanh(C) + C
|
The complex initial string
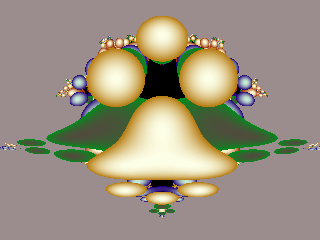
Picture 11.
Formula: Z = Z ^ 2 + C
Initial Z = 0.8 * C * real(C)
|
 To end this short and simple tutorial you have to know, that the initial "Z" value may be a long and complex string, and not only 0 or 1.
To end this short and simple tutorial you have to know, that the initial "Z" value may be a long and complex string, and not only 0 or 1.
In picture 11 I used this complex string:
Z = 0.8 * C * real(C)
More components to play with
| Function | Name |
| recip(Z) | reciprocal |
| sqr(Z) | square |
| sqrt(Z) | square root |
| exp(Z) | exponential |
| log(Z) | natural log |
| abs(Z) | absolute |
|
| Function | Name |
| cabs(Z) | cabs |
| flip(Z) | flip |
| conj(Z) | conjugate |
| real(Z) | real |
| imag(Z) | imaginary |
| | |
|
 Notice that in picture 11 I have used the function real() in the "Z" initialization string. Look at the table below to see all the other math functions that could be used in the same way that we have used all the trig functions.
Notice that in picture 11 I have used the function real() in the "Z" initialization string. Look at the table below to see all the other math functions that could be used in the same way that we have used all the trig functions.
So all that is left for you now is to start practicing and playing with these components, and to enjoy your own creations from A to Z :-))
Go to Chapter III
Dr. Joseph Trotsky, May 2001
|





